By Donald Lancon, Jr.
HIST 4325 / Dr. Swenson
University of Houston
December 5, 1991
(first posted to the web in 1995)
jump to...
Outline of paper
text of paper
Suggestions for further study
Notes
Bibliography
bottom of page
This is a paper I wrote as an undergrad for a History of Science course.
Although it's not publishable or anything,
it's one of my favorite papers because it was so difficult to do.
In fact, the whole History of Science course was quite an experience.
I modified it slightly in certain places as I converted it to HTML (in 1995)
and added links to some related Web-sites at the end of the paper.
Since, at the time, standard HTML didn't include many formatting options,
you will see the caret symbol used to denote exponents (e.g., x^2 = x squared)
and the expression ``sqrt{...}'' to denote square roots
(except for one place where this would make for a really ugly formula --
in this case a GIF image is used
with an ``alt'' tag containing the text version of the formula).
All Greek letters (alpha, beta, ...) are spelled out.
Footnotes (actually, endnotes) appear in square-brackets, like this:
[0].
After following the link to the footnote,
a similar link brings you back to where you started.
Try it with the footnote above.
Okay, here's an outline of the paper.
You may go directly to a section by choosing it in the list below.
Note:
You can also see my
High school Euclid paper,
which was more or less the original version of this paper.
The name of Euclid is often considered synonymous with geometry.
His Elements is one of the most important and influential works
in the history of mathematics,
having served as the basis, if not the actual text,
for most geometrical teaching in the West for the past 2000 years.
It contributed greatly to the ``geometrization'' of mathematics
and set the standard for rigor and logical structure for mathematical works.
[1]
This paper opens with a discussion of what is known about Euclid's life
and his works other than the Elements.
The focus then shifts to a systematic study of the Elements,
examining its content, structure, sources, and place in the
history of mathematics.
Little is known of Euclid's life.
According to Proclus (410-485 A.D.) in his
Commentary on the First Book of Euclid's Elements,
he came after the first pupils of Plato
and lived during the reign of Ptolemy I (306-283 B.C.).
[2]
Pappus of Alexandria (fl. c. 320 A.D.) in his Collection
states that Apollonius of Perga (262-190 B.C.)
studied for a long while in that city under the pupils of Euclid.
[3]
Thus it is generally accepted that Euclid flourished at Alexandria
in around 300 B.C. and established a mathematical school there.
[4]
Proclus also says that Euclid ``belonged to the persuasion of Plato,''
but there exists some doubt as to whether Euclid could truly be called
a Platonist.
[5]
During the middle ages, Euclid was often identified as Euclid of Megara,
due to a confusion with the Socratic philosopher of around 400 B.C.
[6]
Euclid enjoys a reputation as a fair, forthright, and kind individual.
This tradition survives in two famous stories about him.
In one, a student which has just learned his first theorem
asks what he should gain from learning such things;
Euclid tells his slave to give the student three obols,
``since he must make gain out of what he learns.''
[7]
In the other, reported by Proclus,
Ptolemy asks if there is not a quicker way to learn geometry
than studying the Elements,
to which Euclid replies that there is no royal road to geometry.
However, it is likely that this has been appropriated from a similar story
told about Menaechmus (fl. c. 350 B.C.) and Alexander the Great.
[8]
Such tales are useful in displaying the esteem in which Euclid is held,
if nothing else.
In addition to the Elements,
the extant works of Euclid include the Data,
On Divisions of Figures, Phaenomena,
and Optics.
All survive in the original Greek except Divisions,
which is only partially preserved in Arabic.
These works all follow the basic logical structure
of the Elements,
having definitions and rigorously proved propositions.
[9]
The Data is closely related to the first four books of
the Elements.
It opens with definitions of the different senses in which
things are said to be ``given.''
Thus lines, angles, and ratios may be given in magnitude,
rectilinear figures may be given in species or
given in form, points and lines may be given in position,
and so on.
These definitions are followed by 94 propositions
which state that when certain aspects of a figure are given,
other aspects are given.
[10]
For example, proposition 66 states:
``If a triangle have one angle given, the [area of the] rectangle
contained by the sides including the angle has to the [area of the] triangle
a given ratio.''
[11]
Pappus lists this work among those in the Treasury of Analysis;
in fact, the propositions in the Data may be considered
elementary exercises in analysis which supplement the theorems and problems
found in the Elements.
[12]
The Data is also considered important in
the development of algebra.
[13]
The so-called geometrical algebra of the Greeks
is addressed in the discussion of
Book II
of the Elements
in the fourth section of this paper.
On Divisions of Figures survives only in Arabic translation,
although not a direct one.
In its present form, it consists of 36 propositions concerning
the division of various figures into two or more equal parts
or parts in given ratios.
These divisions may be into like figures --
a triangle into two triangles, for example --
or unlike figures --
a triangle into a triangle and a quadrilateral, say.
The figures so divided include triangles, parallelograms, trapezia,
quadrilaterals, circles, and figures bounded by an arc of a circle
and two straight lines which form a given angle.
The proofs of only four propositions have survived.
Two of these are the 19th:
``To divide a given triangle into two equal parts by a line
which passes through a point situated in the interior of the triangle,''
and the 29th:
``To draw in a given circle two parallel lines cutting off
a certain fraction from the circle.''
[14]
This work is similar to the Divisions of Figures
by Heron of Alexandria, writing in perhaps the third century A.D.,
except that Heron supplements his discussion with numerical calculations.
[15]
Euclid's Phaenomena is a tract on sphaeric,
the study of spherical geometry for the purpose of
explaining planetary motions.
[16]
It survives in Greek and is quite similar to
On the Moving Sphere, by Autolycus of Pitane,
who flourished around 310 B.C.
However, the propositions of Autolycus are more abstract
than those of Euclid, who uses the convenient astronomical terms
horizon and circle of the zodiac in his presentation.
The former work also exhibits the ``classical'' Greek form --
discussed in
section III
below -- found in all of Euclid's treatises,
demonstrating that this style of presentation was not original with Euclid,
but was established before his time.
[17]
It is in the Phaenomena that Euclid first makes
the observation that an ellipse may be obtained from cutting a cylinder.
[18]
Euclid's Optics is the earliest surviving Greek treatise
on perspective.
In its definitions Euclid follows the Platonic tradition
that vision is caused by discrete rays which emanate from the eye.
[19]
One important definition is the fourth:
``Things seen under a greater angle appear greater,
and those under a lesser angle less,
while those under equal angles appear equal.''
[20]
In the 36 propositions which follow,
Euclid relates the apparent size of an object to its distance from the eye
and investigates the apparent shapes of cylinders and cones
when viewed from different angles.
Proposition 45 is interesting, proving that for any two unequal magnitudes,
there is a point from which the two appear equal.
Pappus believed such results to be important in astronomy
and included Euclid's Optics, along with the previous work,
Phaenomena, in the Little Astronomy,
a compendium of smaller works to be studied before the Syntaxis
(Almagest) of Claudius Ptolemy.
[21]
Of the lost treatises attributed to Euclid,
four were unquestionably his works:
Conics, Porisms, Pseudaria,
and Surface Loci.
Euclid's Conics predated by a half-century the famous work
by Apollonius on the same subject.
However, Euclid's treatment was most likely a compilation
of previously known information -- much like the Elements --
and was probably not very original.
In fact, according to Pappus, Euclid gave credit to Aristaeus,
a contemporary, for his discoveries in the conics.
[22]
Pappus further states that
``Apollonius, having completed Euclid's four books of conics
and added four others, handed down eight volumes of conics.''
The contents of Euclid's treatise is therefore regarded to have been
quite similar to the first three or four books of Apollonius's work.
The Conics of Apollonius quickly supplanted the former work,
and by the time of Pappus, Euclid's work was already lost,
while that of Aristaeus was still extant.
[23]
Both Pappus and Proclus attribute to Euclid a three-book work called
Porisms, which contained 171 theorems and 38 lemmas.
A porism may be a corollary,
something which follows easily from a proved proposition,
or it may mean a type of proposition intermediate between a theorem --
a statement of the properties of a given thing --
and a problem --
the actual construction or bringing into existence of something.
Proclus gives as an example of the latter meaning
finding the center of a circle
(Proposition I, Book III of the Elements);
the center already exists, but it must be found.
[24]
A third meaning is given by Pappus:
``A porism is that which falls short of a locus-theorem
in respect of its hypothesis.''
[25]
A locus (plural, loci) is a set of points
all of which obey a certain property.
Theorems, problems, and porisms will be discussed further
in the
third section
of this paper.
There have been several attempts to reconstruct the Porisms,
but controversy still rages over the mere meaning of the title,
making discussion of content difficult.
It is generally agreed, however, that the work was in the realm
of higher mathematics.
[26]
Pappus thought it important enough to be included in the
Treasury of Analysis.
[27]
It has been suggested that the entire work was a by-product
of Euclid's investigations into conic sections,
making the propositions contained therein porisms
in the first sense given above.
[28]
Proclus describes a work of Euclid's called Pseudaria,
or Book of Fallacies,
in which he showed beginners how to avoid errors in reasoning by
``setting the true beside the false and adapting his refutations of error
to the seductions we may encounter.''
[29]
It is clear from Proclus's description that the work remained
in the realm of elementary geometry, but nothing else is known about it.
[30]
The last of Euclid's works to be included in the
Treasury of Analysis was Surface Loci.
It is not known whether this title referred to loci on surfaces
or to loci which were themselves surfaces.
Pappus offers two lemmas to this work --
thus they are not part of Euclid's original text --
one of which is the focus-directrix property of conic sections.
The other appears to give loci which are cones or cylinders;
but this interpretation is based on a slight rewording of the lemma
to make it mathematically sound.
In any event, the evidence would appear to favor the interpretation
that the loci were themselves surfaces.
[31]
It is conjectured that some of the loci may have been more complex
quadric surfaces (paraboloids, hyperboloids, prolate spheroids);
however, none of Euclid's original two-book text survives
to confirm such a hypothesis.
[32]
Other works attributed to Euclid include Catoptrica and
several works on music and mechanics.
Catoptrica, on the theory of mirrors,
is attributed to Euclid by Proclus.
It is generally agreed, however, that Proclus was in error.
It is more likely that this work is by Theon of Alexandria
(4th century A.D.), who edited some of Euclid's works.
[33]
Proclus also attributes to Euclid a work called
Elements of Music.
Two extant treatises have been identified with this work:
Introduction to Harmony and Sectio Canonis
(Division of the Scale).
The former is based upon a musical theory of Aristoxenus
and is generally believed to be the work of his pupil Cleonides.
The latter work is based on the Pythagorean theory of mathematical ratios
between musical notes.
It is not a very substantial treatise and is thought by some to be
extracted by a later writer from Euclid's original.
[34]
Several works on mechanics are attributed to Euclid by Arabic sources.
On the Heavy and the Light contains, in nine definitions
and five propositions, Aristotelian notions of moving bodies
and the concept of specific gravity.
A Book on the Balance treats the theory of the lever
in a similarly Euclidean manner, containing one definition, two axioms,
and four propositions.
A third fragment, on the circles described by the ends of a moving lever,
contains four propositions.
These three works complement each other in such a way
that it has been suggested that they are remnants of a single treatise
on mechanics, possibly written by Euclid.
[35]
In the thirteen books of the Elements,
Euclid presents, in an eminently logical way,
all of the elementary Greek geometrical knowledge of his day.
[36]
This includes the theorems and constructions of plane geometry
and solid geometry, along with the theory of proportions,
incommensurables and commensurables, number theory,
and a type of geometrical algebra.
[37]
Proclus defines elements as
``those theorems whose understanding leads to knowledge of the rest.''
[38]
Thus the Elements is a textbook which gathers into one place
the concepts and theorems which constitute the foundation of
Greek mathematics.
Euclid was not the first to write such a work.
It is known that Hippocrates of Chios (fl. c. 440 B.C.) and others
had composed books of elements before him.
[39]
However, Euclid's treatise was quickly recognized
as being superior to all previous Elements
and none of the earlier works have survived.
In Posterior Analytics, Aristotle (384-322 B.C.) presents
a detailed discussion of the role of first principles
in demonstrative sciences.
First principles are those concepts or assertions which remain unproved.
Their truth is assumed and from them other assertions are proved.
[40]
The first principles of Aristotle may be classified into three types:
definitions, axioms, and postulates.
A definition
is a statement which requires only an understanding
of the terms being used.
It says nothing about the existence of the thing being defined;
this must be proved separately.
[41]
For example, defining what is meant by the term ``circle''
does not imply that such an object exists.
An axiom or common notion is an assertion,
the truth of which is taken for granted as being blatantly obvious,
and which is applicable -- by analogy, at least -- in all sciences.
[42]
An example is that things equal to the same thing are equal to each other;
this is the first axiom in the Elements.
Postulates, like axioms, are assumed without proof.
However, whereas modern mathematicians tend not to make any distinction
between the two, the ancient Greeks did.
Aristotle gives three ways of differentiating between postulates and axioms:
[43]
- Postulates are not self-evident, as are axioms.
- Postulates are applicable only to the specific science being considered,
whereas axioms are more general.
- Postulates assert that something exists, whereas axioms do not.
Each of Euclid's postulates may fit any or all of these interpretations.
For example, the postulate
``to describe a circle with any given center and distance'' --
Euclid's third --
is obviously making a statement about the existence of circles
and is not really self-evident, as is the sample axiom given above.
A proposition may be a statement about the properties of an object
or a directive to construct something.
The former type is called a theorem,
the latter a problem.
Theorems do not prove the existence of anything,
since they are conditional statements.
However, problems, once solved,
do prove the existence of something,
since part of the solution is proving that the thing constructed
is indeed an example of the object of interest.
This is one general way of proving existence in mathematics.
For example, to prove the existence of equilateral triangles,
Euclid, in his first proposition, constructs a particular triangle
and proves that its sides are all equal.
Proclus gives six formal divisions of a proposition,
including the enunciation, exposition,
specification, construction, proof,
and conclusion.
He explains:
[44]
Of these the enunciation states what is given
and what is being sought from it,
for a perfect enunciation consists of both of these parts.
The exposition takes separately what is given
and prepares it in advance for use in the investigation.
The specification takes separately the thing that is sought
and makes clear precisely what it is.
The construction adds what is lacking in the given
for finding what is sought.
The proof draws the proposed inference by reasoning scientifically
from propositions that have been admitted.
The conclusion reverts to the enunciation,
confirming what has been proved.
The Greek word translated above as ``specification'' is diorismos.
This term may also mean the conditions of solution, namely
``whether the question proposed is or is not capable of solution,
to what extent it is so capable, and in how many ways.''
[45]
A sample proposition from the Elements
in which all of these concepts are demonstrated is given below.
As with first principles, these ideas were not original with Euclid,
but were developed before his time.
Proposition 22 of Book I
- Enunciation
- Out of three straight lines,
which are equal to three given straight lines, to construct a triangle.
- Diorismos
- Thus it is necessary that two of the straight lines
taken together in any manner should be greater than the remaining one.
[I.20]
- Exposition
- Let the three given straight lines be A, B, C,
and of these let two taken together in any manner
be greater than the remaining one, namely A, B greater than C;
A, C greater than B; and B, C greater than A.
- Specification
- Thus it is required to construct a triangle out of
straight lines equal to A, B, C.
![[figure from I.22]](IMAGES/euclid/eucli22.gif)
- Construction
- Let there be set out a straight line DE,
terminated at D but of infinite length in the direction of E,
and let DF be made equal to A, FG equal to B, and GH equal to C.
[I.3]
With center F and distance FD let the circle DKL be described;
again, with center G and distance GH let the circle KLH be described;
and let KF, KG be joined;
I say that the triangle KFG has been constructed out of three straight lines
equal to A, B, C.
- Proof
- For, since the point F is the center of the circle DKL,
FD is equal to FK.
But FD is equal to A; therefore KF is also equal to A.
Again, since the point G is the center of the circle LKH,
GH is equal to GK.
But GH is equal to C; therefore KG is also equal to C.
And FG is also equal to B;
therefore the three straight lines KF, FG, GK are equal to
the three straight lines A, B, C.
- Conclusion
- Therefore out of the three straight lines KF, FG, GK
which are equal to the three given straight lines A, B, C,
the triangle KFG has been constructed.
Q.E.F.
As discussed earlier, one meaning of the term porism is
a result which follows easily from a proved theorem,
known today as a corollary.
This is the sense of the term as used in the Elements.
A lemma, on the other hand,
is something that is assumed in the proof of a proposition,
but which requires confirmation.
This is usually provided immediately after the conclusion of
the main proposition.
Many of the lemmas which appear in the Elements
are thought to be interpolations by later writers.
Book Definitions Theorems Problems Porisms Lemmas Postulates Axioms
I 23 34 14 1 - 5 5
II 2 12 2 - - - -
III 11 31 6 1 - - -
IV 7 - 16 1 - - -
V 18 25 - 2 - - -
VI 3 23 10 3 - - -
VII 22 33 6 1 - - -
VIII - 25 2 1 - - -
IX - 36 * - 1 - - -
X 16 91 24 4 11 - -
XI 28 34 5 1 1 - -
XII - 16 2 2 2 - -
XIII - 12 6 1 3 - -
Totals 120 372 93 19 16 5 5
- *
- Two propositions are stated as problems, but are actually theorems.
Also in this book is a proposition with no proof.
Book - Previous books or propositions upon which it depends [47]
I - (independent)
II - I
III - I; II.5,6
IV - I; II.11; III
V - (independent)
VI - I; III.27,31; V
VII - (independent)
VIII - V.Def.; VII
IX - II.3,4; VII; VIII
X - I.44,47; II; III.31; V; VI; VII.4,11,26; IX.1,24,26
XI - I; III.31; IV.1; V; VI
XII - I; III; IV.6,7; V; VI; X.1; XI
XIII - I; II.4; III; IV; V; VI; X; XI
Note: All books depend on the axioms in Book I,
so these are not considered in the table.
Prior to the discussion of what is in the Elements,
it must be noted what is not contained in the work.
Firstly, although Euclid uses the concept of rectilinear area extensively,
nowhere does he give a formula for calculating the area of a figure.
The Greeks made a clear distinction between logistic,
which Plato identifies as ``the art of calculation,''
and arithmetic, which is known today as number theory.
[48]
The Elements is completely devoid of logistic.
Secondly,
since Euclid bases his entire geometry on points, straight lines,
and circles (and thus construction by straight-edge and compass alone),
the so-called three famous problems of Greek mathematics --
squaring the circle, doubling the cube, and trisecting the angle --
are not to be found in the work.
Finally, conic sections, known for roughly 50 years
since their discovery by Menaechmus,
were still considered to be in the realm of higher mathematics
in Euclid's time and thus do not appear in the Elements.
[49]
As mentioned above,
Euclid treated conics in a separate work.
In Book I, Euclid defines the basic terms of plane geometry,
including the point, line, surface,
angle, figure, and so forth.
Most of the definitions in this and later books are unremarkable;
however, some merit discussion either for their originality
or for their historical significance.
For example, the way in which Euclid defines point, line, and surface
apparently differs from the definitions given in earlier textbooks.
Aristotle, writing before the time of the Elements,
remarked that in the standard definitions of these objects,
the prior were defined in terms of the posterior;
that is, a point was defined as the extremity of a line,
a line of a surface, and a surface of a solid.
In his view, this made the definitions unscientific.
Euclid, perhaps in response to such criticism,
attempts to define each term independently of the others.
Thus a point is ``that which has no part'' (I.Def.1),
a line is a ``breadthless length'' (I.Def.2),
and a surface is ``that which has length and breadth only'' (I.Def.5).
Having defined each term,
he then reverts to the older definitions to relate the concepts together.
The compromise displayed in these definitions
is thought to be Euclid's own idea.
[50]
Another important definition is the last one of Book I:
``Parallel straight lines are straight lines which,
being produced infinitely in both directions,
do not meet one another in either direction'' (I.Def.23).
This is essentially the same definition as that given by Aristotle.
[51]
Euclid decided not to use another popular definition of parallel lines
as straight lines which are everywhere equidistant from one another.
This definition is crucial to the so-called ``parallel postulate''
(I.Post.5), which has enjoyed a lively history.
This will be discussed further in the next section.
Finally, the terms oblong, rhombus, and rhomboid
are defined, but, curiously, they never appear anywhere else
in the Elements.
It is believed that these are taken from earlier works on the subject.
[52]
The following are the postulates given by Euclid:
- To draw a straight line from any point to any point.
- To produce a finite straight line continuously in a straight line.
- To describe a circle with any center and distance.
- That all right angles are equal to one another.
- That, if a straight line falling on two straight lines
make the interior angles on the same side less than two right angles,
the two straight lines, if produced in-definitely,
meet on that side on which are the angles less than the two right angles.
In the first three postulates, Euclid assumes the existence of
points, lines, and circles.
This is necessary because,
as mentioned earlier,
the definition of these objects
did not imply their existence.
The existence of all other geometrical objects
are proved in later propositions.
The first postulate may also be interpreted as asserting
the uniqueness of the straight line between two given points.
[53]
Similarly, the third is interpreted as asserting
the continuity and infinite extent of space in this way:
the radius of the circle may be indefinitely small,
which implies that there is no minimum distance
between two points in space --
thus space is continuous;
on the other hand, the radius may be indefinitely large,
so there is no maximum distance between two points in space.
It is entirely possible that Euclid saw the ``uniqueness''
interpretation of the first postulate,
but it is doubtful that he interpreted the third in the above manner.
[54]
The fourth and fifth postulates were long thought to be theorems
that could be proved.
The fourth asserts that the right angle is a determinant magnitude,
against which all other angles may be measured.
[55]
The fifth postulate is believed to be original with Euclid.
[56]
It has been called
``the one sentence in the history of science
that has given rise to more publication than any other.''
[57]
The idea that it could be proved was based upon its length and complexity,
and the fact that its converse is a theorem (I.17) that is proved by Euclid.
[58]
A history of the parallel postulate will not be attempted here.
Some of the more notable attempts to prove it are given by Heath
in his edition of the Elements.
[59]
The inability to prove the parallel postulate convinced some,
namely Carl Friedrich Gauss (1777-1855)
and Nicolai Ivanovich Lobachevsky (1793-1856),
that non-Euclidean geometries were possible.
In 1829, Lobachevsky became the first to publish a geometry
built on a postulate which directly contradicted the parallel postulate.
[60]
The five statements given above are the only ones in the Elements
that Euclid identifies as postulates.
However, the fourth and fifth definitions in Book V
have the form of postulates.
[61]
These will be discussed below in the section on
Book V.
The axioms of Euclid, which he calls common notions,
are the following:
- Things which are equal to the same thing are also equal to one another.
- If equals be added to equals, the wholes are equal.
- If equals be subtracted from equals, the remainders are equal.
- Things which coincide with one another are equal to one another.
- The whole is greater than the part.
Of these, only the fourth requires an explanation of Euclid's intent.
It is believed that in this axiom,
he is asserting that superposition is an acceptable method
of proving the equality of two figures.
[62]
Thus in I.4, to prove the so-called ``Side-Angle-Side''
congruence theorem for triangles,
he imagines one triangle to be moved and placed on top of the other,
then shows that all of the sides coincide with one another.
Many other axioms were added by later writers, including:
- (6) Two lines do not enclose a space.
- (7) If equals be added to unequals, the wholes are unequal.
- (8) If equals be subtracted from unequals, the remainders are unequal.
- (9) Doubles of the same thing are equal to one another.
- (10) Halves of the same thing are equal to one another.
However, these are all derivable from Euclid's postulates and axioms.
Note also that ``axiom'' six should actually be a postulate,
since it deals with geometrical objects.
[63]
In the propositions of Book I,
Euclid presents the familiar geometry of lines and angles in the plane,
including results on triangles, intersecting lines, parallel lines,
and parallelograms.
The first three propositions give three fundamental ``operations''
of Euclid's geometry:
- On a finite straight line to construct an equilateral triangle.
- To place at any given point (as an extremity) a straight line equal to a given straight line.
- Given two unequal straight lines, to cut off from the greater a straight line equal to the less.
The majority of the remaining propositions of the Elements
are dependent upon these constructions.
Also contained in the propositions of Book I are
the theorems on congruent triangles,
known to today's high-school geometers as ``Side-Angle-Side'' (I.4),
``Side-Side-Side'' (I.8), ``Angle-Side-Angle'' (I.26),
and ``Angle-Angle-Side'' (also I.26).
The uniqueness of a triangle with given sides is proved in I.7.
In I.22, Euclid shows how to construct a triangle
from any three given lines (provided that it is possible).
That the angles of a triangle sum to two right angles is proved in I.32.
Propositions 9 and 10 call for the bisection of a given angle
and line segment, respectively.
That the opposite angles formed by intersecting lines are equal
is proved in I.15.
Propositions 27-31 deal with parallel lines;
in I.31, Euclid constructs a line parallel to a given line,
passing through a given point not on the line.
The existence of parallelograms is proved in I.33;
following this proposition are many theorems about parallelogrammic figures
and the areas they enclose.
Proposition 42 calls for the construction in a given angle
of a parallelogram equal in area to a given triangle.
This idea is extended in I.45 to the construction in a given angle
of a parallelogram equal in area to a given rectilinear figure.
The construction of a square on a given line is given in I.46.
Finally,
propositions 47 and 48 represent the so-called
Pythagorean Theorem and its converse.
The proof of I.47, based on a figure known as the ``bride's chair,''
is believed to be original with Euclid.
[64]
![[figure from I.47]](IMAGES/euclid/euclbrch.gif)
The ``bride's chair'' from I.47.
The contents of Book II have traditionally been understood
in terms of geometrical algebra.
According to this view, the ancient Greeks took algebraic results
and stated them in geometrical terms, mainly for the sake of rigor.
This has been the dominant view toward ancient Greek mathematics
since it was developed in the 1880's by Hyeronimus Georg Zeuthen
and Paul Tannery.
In the last two decades, however,
this view has undergone severe criticism by those who maintain
that it is not historically valid.
The debate concerning geometrical algebra is still far from over.
[65]
One of the attractions of the geometrical algebra notion
is that it gives a comfortable framework in which to discuss the results
of some of the books in the Elements.
Keeping in mind the foregoing caveat,
the algebraic form of the results in Book II
will be presented here for the sake of convenience.
The first four propositions are the geometrical equivalents
of the following algebraic identities:
[66]
- II.1: a ( b + c + d + ... ) = ab + ac + ad + ...
- II.2: (a + b) a + (a + b) b = (a + b)^2
- II.3: (a + b) a = ab + a^2
- II.4: (a + b)^2 = a^2 + b^2 + 2ab
Propositions 5-10 represent similar, although more complex, identities.
An important proposition, typical of this group, is II.5:
If a straight line be cut into equal and unequal segments,
the rectangle contained by the unequal segments of the whole
together with the square on the straight line between
the points of section is equal to the square on the half.
An example of this proposition is the following,
paraphrased from Euclid's proof:
![[figure from II.5]](IMAGES/euclid/euclii5.gif)
If AB be cut into equal segments at C and into unequal segments at D,
then the area of the rectangle contained by AD and DB (rectangle ADHK),
plus the area of the square on CD (equal to square LHGE),
is equal to the area of the square on CB (square CBFE).
In this case, there are several possible assignments of symbols
to the lengths in the figure,
each of which gives rise to a different algebraic identity.
This displays one problem with the idea that the Greeks of Euclid's time
had the notion of algebra.
The geometrical statement and proof of this theorem is unambiguous.
However, there are many different ways of algebraically representing
this theorem.
It may be seen as the geometrical equivalent of either of the identities
(a + b) (a - b) + b^2 = a^2
or
ab + [(a + b) / 2 - b]^2 = [(a + b) / 2]^2
or as the basis of a geometrical solution of the equation
ax - x^2 = b^2.
[67]
Sabetai Unguru, in his controversial article
``On the Need to Rewrite the History of Greek Mathematics,''
decries such interpretations;
he argues forcefully that the Greeks were not using the equivalent
of our algebra, but that
``[it] is we who are using algebra...
as the equivalent of their geometry!''
[68]
Unguru is one of the more outspoken critics of the traditional view.
In II.12 and II.13, Euclid presents the geometrical equivalent
of today's ``law of cosines'':
a^2 = b^2 + c^2 - 2 bc cos A ,
where A is the angle opposite side a.
In the figure below, given by Euclid,
``the square on AC is less than the squares on CB, BS
by twice the rectangle contained by CB, BD''
(from II.13).
![[figure from II.13]](IMAGES/euclid/euclii13.gif)
Finally, in II.14, Euclid calls for the construction of a square
equal in area to a given rectilinear figure.
In general, this is the problem of quadrature.
As mentioned before,
Euclid does not apply this method to curvilinear figures,
although Hippocrates of Chios had ``squared'' the lune --
a crescent-shaped figure bounded by two circular arcs --
over a hundred years before.
[69]
Book III deals with circles, segments of circles, and sectors of circles
(see figures below).
Several of the propositions are regarded as not entirely satisfactory today.
The proofs of some seem to be lacking in clarity, if not rigor;
some rely on unproved assumptions;
and others suffer from Euclid's tendency to avoid multiple cases
in his proofs.
In any event, modern textbooks tend to present the material on circles
differently from Euclid.
[70]
![[figure]](IMAGES/euclid/eucliii.gif)
ABF and CDE are segments of the first circle.
GHK is a sector of the second circle.
In III.1, Euclid finds the center of a given circle.
Propositions 5 and 6 prove that two circles will not have the same center
if they either cut (III.5) or touch (III.6) each other.
Several theorems deal with the ways in which circles may or may not
cut or touch each other.
For example, that circles do not cut each other at more than two points
is demonstrated in III.10.
Proposition 16, about lines tangent to a circle,
is historically interesting.
It states:
[71]
The straight line drawn at right angles to the diameter of a circle
from its extremity will fall outside the circle,
and into the space between the straight line and the circumference
another straight line cannot be interposed;
further the angle of the semicircle is greater, and the remaining angle less,
than any acute rectilineal angle.
![[figure from III.16]](IMAGES/euclid/eucliiix.gif)
In the figure above, the tangent EF is drawn at the extremity of BE,
the angle of the semicircle is angle DEC,
and the remaining angle is angle DEF.
The last part of this theorem introduces the problem of
the nature of angles formed by curved lines and straight lines,
especially tangents.
There was great controversy over this subject in the 13th to 17th centuries,
before the development of calculus gave a rigorous way
of dealing with tangents, instantaneous slopes of curves, and the like.
[72]
Proposition 17 demonstrates how to draw a tangent to a circle
from any given point outside the circle.
In III.20 it is proved that an angle at the circumference of a circle
is double the angle at the center
when the two angles have the same circumference as a base (see figure below).
That all angles inscribed in the same circular segment are equal
is proved in III.21 (see figure).
The circular arc is bisected in III.30.
The penultimate theorem of Book III (the 37th) states that
if two straight lines be drawn from a single point outside of a circle,
one touching it and the other cutting it,
then the rectangle contained by the whole of the cutting line
and the segment external to the circle
is equal to the square on the tangent line (see figure).
![[figures from III.20, III.21, III.37]](IMAGES/euclid/eucliii3.gif)
III.20: angle ADC = 2 angle ABC
III.21: angle EGF = angle EHF
III.37: (beta + gamma) gamma = alpha^2
The fourth book is concerned with figures circumscribed about
or inscribed within circles.
All of the propositions are problems,
specifying constructions to be carried out.
There are four possible constructions for each figure:
- Given a circle to inscribe a given figure.
- Given a circle to circumscribe a given figure.
- Given a figure to inscribe a circle.
- Given a figure to circumscribe a circle.
The figures so treated include a triangle of any shape (IV.2-5),
a square (IV.6-9), a regular pentagon (IV.11-14), a regular hexagon (IV.15),
and a regular 15-sided figure (IV.16).
In Book V, Euclid presents the theory of proportions
generally attributed to Eudoxus of Cnidus (died c. 355 B.C.).
This theory does not require commensurability --
that is, the use of numbers that have a common divisor --
and is therefore superior to the Pythagorean theory based on integers.
Euclid presents the Pythagorean theory in
Book VII.
[73]
Books I, V, and VII are the only books in the Elements
that are entirely self-contained, being
dependent
on no other books.
Any of them could have served as
the starting point for the treatise;
it is therefore significant that Euclid chose
the purely geometrical Book I as the foundation for the whole work.
[74]
This fact may be used as another argument against
the geometrical algebra view.
Euclid apparently puts off the discussion of proportion as long as possible,
even though it lends itself naturally to algebraic methods.
Two of the definitions in this book are of particular importance.
According to the
fourth definition,
``Magnitudes are said to have a ratio to one another
which are capable, when multiplied, of exceeding one another.''
That is, A and B have a ratio if nA > B for some integer n
and mB > A for some integer m; thus A and B are finite and non-zero.
This is essentially the so-called ``Axiom of Archimedes,''
which Archimedes himself attributes to Eudoxus.
[75]
The fifth definition -- of magnitudes being in the same ratio --
is also very important, saying essentially that A : B :: C : D
(read ``A is to B as C is to D'')
if given any two integers m and n, mC < nD when mA < nB,
mC = nD when mA = nB, and mC > nD when mA > nB.
[76]
Other definitions present various terms used in the transformation of ratios,
including alternate ratio, inverse ratio,
composition of a ratio, separation of a ratio,
conversion of a ratio, ratio ex aequali,
and perturbed proportion.
For example, composition of a ratio means
the transformation of the ratio A : B into the ratio A + B : B.
These definitions simply give names to various manipulations of ratios.
All of the propositions in Book V are theorems.
They address multiples of magnitudes, ratios of magnitudes,
and magnitudes in given proportions.
Most are obvious when expressed in modern symbology.
In this case, however, the modern notation is not misleading,
since Euclid himself often uses letters to stand for magnitudes.
Three examples of the types of propositions contained in this book
are the following:
- V.4: If A : B :: C : D, then mA : nB :: mC : nD, for any integers m and n.
- V.17: If A : B :: C : D, then (A - B) : B :: (C - D) : D.
(This is an example of separation of ratios.)
- V.21: If A : B :: E : F and B : C :: D : E, then D < F if A < C,
D = F if A = C, and D > F if A > C.
(The conclusion of this proposition may also be stated A : C :: D : F.)
Book VI deals with similar rectilinear figures
and extends the technique of transformation of areas developed in Book I
into the method of application of areas,
a major constituent of the geometrical algebra view of Greek mathematics.
The first definition of this book states:
``Similar rectilineal figures are such as have their angles
severally equal and the sides about the equal angles proportional''
(VI.Def.1).
The dependence of the theory of similar figures on proportions
is the reason why the theorems of similarity do not appear in Book I.
In VI.1 it is proved that triangles of the same height
``are to one another as their bases'' --
i.e., that their bases and areas are proportional.
Propositions 4-7 concern similar triangles.
In VI.11, Euclid finds a third proportional
to two given straight lines --
i.e., given A and B, find C such that A : B :: B : C.
In VI.12, he finds a fourth proportional to three given lines --
given A, B, and C, find D such that A : B :: C : D.
Finally, in VI.13, he finds a mean proportional
between two given lines --
given A and B, find C such that A : C :: C : B.
Several theorems follow concerning figures
whose sides are in various proportions.
Proposition 18 calls for the construction on a given straight line
of a figure ``similar and similarly situated to a given rectilineal figure.''
Another powerful technique in the transformation of areas is given in VI.25:
``To construct one and the same figure similar to a given rectilineal figure
and equal [in area] to another given rectilineal figure.''
An example of this would be to construct a quadrilateral
similar to a given quadrilateral, but equal in area to a given triangle.
Propositions 28 and 29 are examples of the method of
application of areas.
This is a controversial subject,
since the traditional interpretation of this technique
is that the Greeks used it to solve quadratic equations.
(Transformation of areas, by the way,
is not controversial in the least, since it simply means
constructing one figure equal in area to another figure.)
An example of application of areas is VI.29:
``To a given straight line to apply a parallelogram
equal to a given figure and exceeding by a parallelogrammic figure
similar to a given one.''
![[figure from VI.29]](IMAGES/euclid/euclvi29.gif)
In terms of the figure above, given straight line AB, figure C of given area,
and figure D of given shape, the problem is to apply to AB a figure (AEFH)
equal in area to C and exceeding by a figure (BEFG) similar to D.
According to those who hold the geometrical algebra view,
the Greeks used this construction to solve quadratics of the form
ax + b/c x^2 = S,
where the parallelograms are taken to be rectangles,
and where a = AB, x = BG, b/c is the ratio formed by the sides of D,
and S is the area of C.
[77]
Personally, I find it hard to believe that Euclid himself, at least,
had any notion of the algebraic equivalent
to his geometrical problem.
This is supported by the statement of Proclus that
``the application of areas, their exceeding and falling short
[are] ancient discoveries of the Pythagorean muse,''
implying a date of discovery long before Euclid's time.
[78]
Thus their origin is surely not algebraic in nature.
In VI.30, a line is cut in extreme and mean ratio.
This means cutting a straight line into unequal segments
so that the smaller segment is to the larger as the larger is to the whole.
This construction, known today as the golden section,
appears again in
Book XIII.
Proposition 31 is a generalization of the
Pythagorean Theorem
of Book I:
``In right-angled triangles the figure on the side subtending the right angle
is equal to [the sum of the areas of] the similar and similarly described
figures on the sides containing the right angle.''
Note that the figures in this proposition may be of any shape.
According to Proclus, this theorem is original with Euclid.
[79]
In Book VII, Euclid presents Pythagorean number theory.
This is the last book of the Elements
that is entirely
self-contained.
The first definition is of the unit, being
``that by virtue of which each of the things that exist is called one.''
Definition 2 states that
``a number is a multitude composed of units.''
Thus the Pythagorean concept of number includes only
integers greater than one.
Subsequent definitions subdivide the set of numbers
into smaller categories of numbers:
even and odd;
even-times even (e.g., 4=2x2),
even-times odd (6=2x3),
and odd-times odd (15=3x5);
composite and prime;
plane and solid
(the products of two and three numbers, respectively);
square and cube;
and perfect (number equal to the sum of its divisors,
as 28 = 1 + 2 + 4 + 7 + 14).
Euclid also defines what it means for numbers to be
prime to one another -- relatively prime numbers --
and composite to one another -- numbers which have a common divisor.
These definitions serve as the basis for Books VII-IX,
the so-called ``arithmetical'' books,
which are almost entirely
independent
of the first six books.
[80]
Propositions 2 and 3 give a method for finding the greatest common divisor
of two and three numbers, respectively.
Propositions 4-20 set out the Pythagorean theory of proportion
based on commensurables, numbers which have a common divisor.
Most of these theorems are direct analogs of those in Book V,
which deals with general magnitudes.
However, Euclid does not treat them as
special cases of the earlier theorems,
but instead proves all of them from the principles of commensurability.
Primes and relative primes are treated in VII.21-32.
For example, in VI.31 it is proved that any composite number is
``measured by'' (has as a divisor) some prime number.
Least common multiples are discussed in VII.34-39.
Here appear problems on finding the least common multiple of two (VII.34)
or three (VII.36) numbers.
The method employed may be extended to find the least common multiple
of as many numbers as desired.
[81]
The propositions of this book deal with numbers in continued proportion;
that is, geometrical progressions of the form
a, ab, ab^2, ab^3, ab^4, ... .
A typical proposition is VIII.1, which states:
``If there be as many numbers as we please in continued proportion,
and the extremes of them be prime to one another,
the numbers are the least of those which have the same ratio with them.''
That is, if A, B, C, ... N be a geometrical sequence such that
A and N are relatively prime,
then there exists no other sequence of integers A', B', C', ... N'
with the same common ratio such that A' < A, B' < B, ... N' < N.
[82]
The remaining propositions are along similar lines,
dealing with square, cube, plane, and solid numbers in continued proportion.
The last of the so-called ``arithmetical'' books
deals mainly with multiplication and the classification of numbers
in geometric progressions from the unit --
that is, sequences of the form
1, a, a^2, a^3, a^4, ... .
Proposition 14 is the fundamental theorem in number theory
that a number may be resolved into prime factors in only one way.
[83]
In IX.20, Euclid proves that
``prime numbers are more than any assigned multitude of prime numbers'' --
that is, that the number of primes is (countably) infinite.
Propositions 21-29 deal with the sums, differences, and products
of odd and even numbers taken in different combinations.
In proposition 36, Euclid proves that if
1 + 2 + 4 + 8 + 16 + ... + 2^n = S
be prime, then S 2^n will be a perfect number.
This is still the only known method for finding perfect numbers.
[84]
Most of this book is devoted to the classification of irrationals.
According to a commentary by Pappus on this book,
much of the theory is due to Theaetetus (425-369 B.C.).
[85]
It is considered the most difficult book of the Elements
and is by far the longest at 115 propositions.
Euclid's notions of rational and irrational are slightly different
from those of today.
According to the third definition,
a rational line is any which is commensurable in length
or in square to a given reference line,
which is a priori agreed to be rational.
Hence, if P is assumed to be rational,
then given any proper fraction M/N that is not the square
of another proper fraction (as is 1/4 = 1/2 x 1/2),
Euclid would call both
M/N P
and
sqrt{M/N} P
rational, whereas today's mathematician would identify the latter quantity
as irrational.
According to Heath, Euclid differed from his predecessors
in this extension of the concept of rational quantities.
[86]
In the first Proposition of Book X, Euclid gives the theorem
that serves as the basis of the method of exhaustion
credited to Eudoxus.
The theorem states:
Two unequal magnitudes being set out,
if from the greater there be subtracted a magnitude greater than its half,
and from that which is left a magnitude greater than its half,
and if this process be repeated continually,
there will be left some magnitude which will be less than
the lesser magnitude set out.
This result depends on
definition 4 of Book V,
the so-called Axiom of Archimedes.
It is this theorem which allows Euclid to compare
the areas of curvilinear figures and volumes of solids in Book XII.
In X.21, Euclid begins classifying irrationals.
The first category is arrived at in this way:
if the sides of a rectangle be commensurable in square only
(e.g., 3 and sqrt{2}), then the side of the square equal to the rectangle
(3 sqrt{2}, in this case) is an irrational called medial.
The rest of Book X is devoted to naming and proving theorems about medials
and 24 other types of irrationals.
In modern algebraic symbology, all of these are of the form
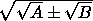
Irrationals of this form with a plus sign are called binomials
(discussed in X.36-72)
and those with the minus, apotomes (X.73-110).
[87]
In X.111, it is proved that a magnitude connot be both
a binomial and an apotome.
This book contains the final group of definitions,
all of which concern solid geometry.
Euclid departs from tradition in many of his definitions of solid figures.
For example, Aristotle defines a sphere as a solid whose
``extremity is equally distant from its center.''
[88]
Euclid, however, defines a sphere as
a figure described by the revolution of a semicircle about its fixed diameter
(XI.Def.14).
Similar ``motion-based'' definitions are given for
the cone (XI.Def.18) and cylinder (XI.Def.21).
Other definitions concern parallel planes,
similar and equal solid figures, solid angles,
prisms, pyramids,
and the other four regular solids --
the tetrahedron is not distinguished from the pyramid.
The propositions of Book XI begin with the elementary theorems
of three-dimensional geometry:
that two planes but each other in a line (XI.3),
that two lines at right angles to a given plane
are parallel to each other (XI.6), and so on.
Two typical problems are to drop a perpendicular to a given plane
from a point not on that plane (XI.11) and to construct a solid angle
from three given plane angles, if possible (XI.23).
The latter third of the book is devoted mainly to
parallelepipedal solids, which are solids contained by
three pairs of parallel planes.
[89]
![[figure]](IMAGES/euclid/euclppps.gif)
Parallelepipedal solids.
Book XII concentrates on pyramids, cones, and cylinders.
It is in this books that Euclid employs the celebrated
method of exhaustion.
Since this method is attributed to Eudoxus,
it is assumed that most of this book is due to him.
[90]
After proving that
``similar polygons inscribed in circles are to one another
as the squares on the diameters [of the circles]'' (XII.1),
Euclid uses the result and the method of exhaustion to prove that
circles themselves are to one another
as the squares on the diameters (XII.2).
This is accomplished by assuming that the circles do not obey this property
and getting a contradiction.
By inscribing a square in each circle, then an octagon,
then a 16-sided figure, and so on, it is shown that eventually
one will obtain polygons that are not to one another
as the squares on the diameters.
Thus the assumption is wrong and the proposition is proved correct.
The method of exhaustion is also used to prove that pyramids, cones,
and cylinders of the same height are to one another --
with respect to their volumes --
as their bases (XII.5, XII.11)
and that a cone is one third of a cylinder with the same base and height
(XII.10).
Proposition 17 foreshadows the construction of the five regular solids
in Book XIII:
``Given two spheres about the same center,
to inscribe in the greater sphere a polyhedral solid
which does not touch the lesser sphere at its surface.''
Euclid uses this in the final proposition (XII.18)
to prove that spheres are to one another as the cubes on their diameters.
The final genuine book of the Elements is devoted to
the construction of the five regular solids.
Much of this book is assumed to be based on a work by Aristaeus
entitled Comparison of the Five Figures.
[91]
The construction of these so-called ``Platonic figures''
was thought by Proclus to be the objective of the entire work --
a view which supported his contention that Euclid was a Platonist.
[92]
However, there is no real significance to
the placement of the regular solids in the final book.
The propositions of this book had to come last
because they
depend
on most of the preceding books.
On the other hand,
Euclid could have easily skipped the ``arithmetical'' books (VII-IX)
if his purpose was merely the construction of the regular solids.
Book XIII begins humbly enough with six propositions on lines being cut
in extreme and mean ratio -- that is, in the golden ratio.
This ratio arises in regular pentagons
and is therefore necessary for the discussion of the dodecahedron.
Various propositions follow concerning pentagons, hexagons,
and equilateral triangles inscribed in circles.
Finally, Euclid constructs in spheres the five regular solids:
the tetrahedron, composed of four equilateral triangles
and called by Euclid a pyramid (XIII.13);
the octahedron, of eight equilateral triangles (XIII.14);
the cube (XIII.15);
the icosahedron, of twenty equilateral triangles (XIII.16);
and the dodecahedron, of twelve regular pentagons (XIII.17).
Finally, in XIII.18, Euclid sets out in the same semicircle
the sides of the five figures and compares them to one another.
Also in this proposition he proves that
no other regular polyhedra are possible.
![[figure]](IMAGES/euclid/eucl5rs.gif)
The five regular solids.
A fourteenth book was added to Euclid's original thirteen by Hypsicles
(fl. c. 170 B.C.).
Working from treatises by Aristaeus and Apollonius,
he compares the five regular solids with respect to their faces,
surface areas, and volumes.
[93]
A fifteenth book is due to Isadorus of Miletus (c. 530 A.D.),
perhaps written down by one or more of his students.
It deals with inscribing certain of the regular solids in others,
determining the number of edges and vertices on each solid,
and finding the angle of inclination between adjacent faces in each solid.
This so-called ``Book XV'' is quite inferior to the previous one,
being imprecise and even inaccurate in some passages.
[94]
For those desiring to know more about Greek mathematics in general
or Euclid in particular, I have appended this short list of sources
grouped, somewhat arbitrarily, by general subject matter.
The emphasis is on book-length works,
although some journal articles are included.
All selections are in English.
jump to...
General bibliographies
On the History of Mathematics
On the History of Greek Mathematics
On Greek Geometry and Analysis
Euclid's Predecessors and Commentators
The Works of Euclid
On Euclid and His Works
A Debate Over Geometrical Algebra
On Other Related Topics
Web-Sites
- Joseph W. Dauben,
The History of Mathematics from Antiquity to the Present /
A Selective Bibliography.
(New York: Garland Publishing, Inc., 1985)
Lists over 2,000 titles in the history of mathematics;
arranged by topic; with name index.
See also the bibliographies in the
DSB articles
by Bulmer-Thomas and Murdoch,
especially if interested in non-English sources.
- Carl B. Boyer and Uta C. Merzbach,
A History of Mathematics,
2nd ed. (New York: John Wiley & Sons, 1989)
Merzbach's revision of 1968 original by Boyer;
written in textbook style, with exercises at the end of each chapter;
8 of 28 chapters on Greek mathematics.
- Florian Cajori,
A History of Elementary Mathematics
(London: Maximillian, 1897)
Arranged by subject matter and geography;
one chapter on geometry and trigonometry;
places Euclid in the context of the various ``schools'' of Greek mathematics.
- Morris Kline,
Mathematical Thought from Ancient to Modern Times,
Vol. I (NY: Oxford University Press, 1972)
Though not used as a source for this paper,
treatment of Euclid and his Elements is very similar;
six chapters cover Greek mathematics.
- Sir Thomas L. Heath,
A History of Greek Mathematics,
2 vols. (New York: Dover Publications, 1981)
The standard work (in English) on the subject;
Volume I: Thales to Euclid; Volume II: Aristarchus to Diophantus.
- James Gow,
A Short History of Greek Mathematics
(Cambridge?, 1884)
Arrangement based on the concepts of logistic and arithmetic and ``schools'';
chapter on Euclid, Archimedes, and Apollonius.
- D. H. Fowler,
The Mathematics of Plato's Academy: A New Reconstruction
(Oxford: Clarendon Press, 1987)
Contains more ``mathematical'' treatment of Euclid
in the context of the school of Plato; emphasis on ratio and proportion.
- A. Szabo,
The Beginnings of Greek Mathematics
(D. Reidel, 1968)
Concentrates on the philosophical and logical aspects
of early Greek mathematics;
discusses concepts such as first principles and the nature of proof.
- J. L. Berggren,
``History of Greek Mathematics: A Survey of Recent Research,''
Historia Mathematica 11 (1984)
Review of research in the Greek axiomatic method, analysis,
geometrical algebra, theory of proportion, incommensurables, and other topics.
- S. H. Gould,
``The origins of Euclid's Axioms,''
The Mathematical Gazette 46 (1962)
Discusses the birth of the axiomatic method in geometry
and Euclid's parallel postulate.
- M. S. Mahoney,
``Another Look at Greek Geometrical Analysis,''
Archive For History of Exact Sciences 5 (1968)
Discusses problems of logical rigor and the concepts of diorismos,
reductio ad absurdum, and porisms, using various exmaples from Pappus,
Archimedes, and several works of Euclid.
- W. R. Knorr,
The Evolution of the Euclidean Elements
(Dordrecht, Holland: D. Reidel, 1975)
Devoted mainly to the concept of incommensurability up to the time of Euclid.
- Sir Thomas L. Heath,
Mathematics in Aristotle
(Oxford: Clarendon Press, 1970)
Aristotle's views on ``first principles'' and pre-Euclidean Greek mathematics;
Prior Analytics, Posterior Analytics,
Topics and other works.
- Pappus of Alexandria,
Book 7 of the Collection,
2 vols., trans. Alexander Jones (NY: Springer Verlag, 1986)
Includes information on Euclid's Surface Loci,
Data, and Porisms;
includes attempted reconstruction of the latter work.
- William Thompson and Gustav Junge,
The Commentary of Pappus on Book X of Euclid's Elements
(Cambridge?, 1930)
- Proclus,
A Commentary on the First Book of Euclid's Elements,
trans. Glenn R. Morrow (Princeton: Princeton University Press, 1970)
Based on Gottfried Friedlein's Greek text; 30-page introduction.
- Sir Thomas L. Heath,
The Thirteen Books of Euclid's Elements,
2nd ed. (New York: Dover Publications, 1956)
Unabridged English translation from Heiberg's authoritative Greek text;
151-page introduction and copious notes, including textual
and historical analysis of almost every definition and proposition;
the standard English edition.
- Euclid,
The Medieval Latin Translation of the Data of Euclid,
ed. and trans. Shuntaro Ito (Boston: Birkhauser, 1980)
Slightly edited Latin version of the work with concurrent English translation.
- Ivor Bulmer-Thomas,
``Euclid,''
Dictionary of Scientific Biography (1971)
Scholarly review of Euclid's works; extensive bibliography.
- John Murdoch,
``Euclid: Transmission of the Elements,''
Dictionary of Scientific Biography (1971)
Traces the transmission of the Elements through history;
extensive bibliography.
- I. Mueller,
Philosophy of Mathematics and Deductive Structure
in Euclid's Elements
(Cambridge: MIT Press, 1981)
Study of the mathematics of the Elements
and the sequence of ideas in the work;
unabashed in its use of modern mathematical notations and concepts.
- George W. Evans,
``Postulates and Sequence in Euclid,''
The Mathematics Teacher 20 (1927)
Investigates the dependence of each book in the Elements
on preceding ones.
- George W. Evans,
``Some of Euclid's Algebra,''
The Mathematics Teacher 61 (1968)
Discusses geometrical algebra view of various propositions of
the Elements, with emphasis on Books II, VI, and X.
- Marshall Clagget,
``The Medieval Latin Translations From the Arabic
of the Elements of Euclid,
With Special Emphasis on the Versions of Adelard of Bath,''
Isis 44
- Sabetai Unguru,
``On the Need to Rewrite the History of Greek Mathematics,''
Archive for History of Exact Sciences 15 (1975)
Severely criticizes the ``geometrical algebra'' view of Greek mathematics;
lots of exclamation points!
- B. L. Van der Waerden,
``Defence of a `Shocking' Point of View,''
Archive for History of Exact Sciences 15 (1976)
A sober, scholarly rejoinder to Unguru (1975).
- H. Freudenthal,
``What is Algebra and What Has It Been in History?''
Archive for History of Exact Sciences 16 (76)
Another response to Unguru (1975).
- Andre Weil,
``Who Betrayed Euclid?''
Archive for History of Exact Sciences 19 (1978)
A vitriolic response to Unguru (1975), whom he calls author ``Z''!
- Sabetai Unguru,
``History of Ancient Mathematics / Some Reflections on the State of the Art,''
Isis 70 (1979)
- Roger Herz-Fischler,
A Mathematical History of Division in Extreme and Mean Ratio
(Waterloo, Ontario: Wilfred Laurier University Press, 1987)
Apparently the standard work on the subject;
the history of the golden section from the time of the ancient Egyptians
and Babylonians to the 18th century.
- H. E. Huntley,
The Divine Proportion: A Study in Mathematical Beauty
(NY: Dover, 1970)
A popular account; the golden ratio in mathematics, art, and nature.
- [0]
- Okay, now you can follow this link back to where you started.
- [1]
- Ivor Bulmer-Thomas,
``Euclid,'' DSB (1971), p. 424.
- [2]
- Proclus,
A Commentary on the First Book of Euclid's Elements,
trans. Glenn R. Morrow (Princeton: PUP, 1970), p. 56 [68:11];
Sir Thomas L. Heath,
The Thirteen Books of Euclid's Elements,
2nd ed. (1926; rpt. New York: Dover Publications, 1956), I, p. 2;
Carl B. Boyer and Uta C. Merzbach,
A History of Mathematics,
2nd ed. (New York: John Wiley & Sons, 1989), p. 213.
Concerning Heath's edition of the Elements,
I have chosen to cite references from Euclid's text
in parentheses in the text of my paper
by book and proposition (or definition, etc.) number;
references to Heath's introduction or commentary
are documented in these footnotes;
also, all figures presented in this paper are based upon figures
in Heath's Elements.
- [3]
- Heath, Elements,
I, p. 2;
Boyer,
p. 160, 207.
- [4]
- Heath, Elements,
I, p. 2.
- [5]
- Proclus,
p. 57 [68:19-20];
Bulmer-Thomas,
p. 415.
- [6]
- Heath, Elements,
I, p. 3.
- [7]
- Heath, Elements,
I, p. 3;
Bulmer-Thomas,
p. 415.
- [8]
- Heath, Elements,
I, p. 1;
Boyer,
p. 97.
- [9]
- Boyer,
p. 117-8;
Bulmer-Thomas,
p. 425-30.
- [10]
- Bulmer-Thomas,
p. 425.
- [11]
- Sir Thomas L. Heath,
A History of Greek Mathematics
(1921; rpt. New York: Dover Publications, 1981), I, p. 424.
- [12]
- Heath, Elements,
I, p. 8.
- [13]
- B. L. Van der Waerden,
Science Awakening I,
trans. Arnold Dresden (Groningen, Holland: P. Noordhoff, [1975?]), p. 198.
- [14]
- Bulmer-Thomas,
p. 426;
Heath, Greek,
I, p. 425-6.
- [15]
- Heath, Elements,
I, p. 8, 21;
Heath, Greek,
II, p. 337.
- [16]
- Heath, Greek,
I, p. 11-12.
- [17]
- Heath, Greek,
I, p. 348-52.
- [18]
- Heath, Greek,
I, p. 111.
- [19]
- Bulmer-Thomas,
p. 430.
- [20]
- Heath, Greek,
I, p. 442;
my emphasis, to specify what is being defined.
- [21]
- Heath, Greek,
I, p. 441-3;
Bulmer-Thomas,
p. 430;
Heath, Greek,
II, p. 396.
- [22]
- Heath, Greek,
II, p. 116-7;
Boyer,
p. 116.
- [23]
- Bulmer-Thomas,
p. 427;
the quote earlier in the paragraph is also from this source.
- [24]
- Bulmer-Thomas,
p. 426.
- [25]
- Heath, Greek,
I, p. 431-2.
- [26]
- Heath, Elements,
I, p. 14-15.
- [27]
- Heath, Greek,
I, p. 431.
- [28]
- Bulmer-Thomas,
p. 427.
- [29]
- Proclus,
p. 59 [72:3].
- [30]
- Heath, Greek,
I, p. 430.
- [31]
- Heath, Greek,
II, p. 426;
Heath, Elements,
I, p. 15.
- [32]
- Bulmer-Thomas,
p. 429.
- [33]
- Bulmer-Thomas,
p. 430;
Heath, Greek,
II, p. 526-8.
- [34]
- Bulmer-Thomas,
p. 430-1.
- [35]
- Bulmer-Thomas,
p. 431;
Heath, Greek,
I, p. 445-6.
- [36]
- Boyer,
p. 119.
- [37]
- Boyer,
p. 128-32;
there is much controversy surrounding the concept of geometrical algebra;
see the discussion of
Book II
in section IV of this paper.
- [38]
- Proclus,
p. 59 [72:3].
- [39]
- Heath, Elements,
I, p. 116;
Heath, Greek,
I, p. 183.
- [40]
- Heath, Elements,
I, p. 117.
- [41]
- Heath, Elements,
I, p. 118, 143.
- [42]
- Heath, Elements,
I, p. 117-9.
- [43]
- Heath, Elements,
I, p. 117-9.
- [44]
- Proclus,
p. 159 [203:5-14]; my emphasis.
- [45]
- Proclus,
p. 158 [202:4-5];
Heath, Elements,
I, p. 130.
- [46]
- Text and figure copied exactly from
Heath, Elements,
I, p. 292-3;
I added the labels (``Enunciation,'' etc.).
- [47]
- George W. Evans,
``Postulates and Sequence in Euclid,''
The Mathematics Teacher 20 (1927), 316.
- [48]
- Heath, Greek,
I, p. 13-14.
- [49]
- Heath, Greek,
I, p. 251;
Boyer,
p. 119.
- [50]
- Heath, Elements,
I, p. 155, 165.
- [51]
- Heath, Elements,
I, p. 190.
- [52]
- Heath, Elements,
I, p. 151.
- [53]
- Heath, Elements,
I, p. 195.
- [54]
- Heath, Elements,
I, p. 199-200.
- [55]
- Heath, Elements,
I, p. 200.
- [56]
- Heath, Greek,
I, p. 375.
- [57]
- S. H. Gould,
``The origins of Euclid's Axioms,''
The Mathematical Gazette 46 (1962), 284.
- [58]
- Gould,
p. 285;
Heath, Greek,
II, p. 227.
- [59]
- Heath, Elements,
I, p. 220.
- [60]
- Boyer,
p. 558, 580-2.
- [61]
- Evans, ``Postulates,''
p. 316-7.
- [62]
- Heath, Elements,
I, p. 225.
- [63]
- Heath, Elements,
I, p. 223, 232.
- [64]
- Heath, Greek,
I, p. 378;
Heath, Elements,
I, p. 417.
- [65]
- Bulmer-Thomas,
p. 436;
Sabetai Unguru,
``On the Need to Rewrite the History of Greek Mathematics,''
Archive for History of Exact Sciences 15 (1975), 69, 71;
J. L. Berggren,
``History of Greek Mathematics: A Survey of Recent Research,''
Historia Mathematica 11 (1984), 398.
- [66]
- Heath, Elements,
I, p. 372.
- [67]
- Heath, Elements,
I, p. 373, 383.
- [68]
- Unguru,
p. 108; his emphasis.
- [69]
- Boyer,
p. 76.
- [70]
- Heath, Elements,
II,
various places in his discussion of Book III, p. 1-77.
- [71]
- Heath, Elements,
II, p. 37;
the reason for this footnote is the word ``rectilineal''
in the statement of the proposition;
Heath uses this word, so I will use it in direct quotes;
but in my own text, I will use the more common ``rectilinear.''
- [72]
- Heath, Elements,
II, p. 39.
- [73]
- Heath, Elements,
II, p. 112-3;
Boyer,
p. 97.
- [74]
- Evans, ``Postulates,''
p. 314.
- [75]
- Boyer,
p. 102.
- [76]
- Boyer,
p. 102.
- [77]
- Heath, Elements,
II, p. 266.
- [78]
- Proclus,
p. 332 [419:11-14]; my emphasis.
- [79]
- Heath, Elements,
II, p. 269.
- [80]
- Evans, ``Postulates,''
p. 316-7.
- [81]
- Heath, Elements,
II, p. 341.
- [82]
- Heath, Elements,
II, p. 346.
- [83]
- Bulmer-Thomas,
p. 421.
- [84]
- Boyer,
p. 131.
- [85]
- Heath, Greek,
I, p. 209.
- [86]
- Heath, Elements,
III, p. 11-12.
- [87]
- Bulmer-Thomas,
p. 422;
George W. Evans,
``Some of Euclid's Algebra,''
The Mathematics Teacher, 20 (1927);
rpt. The Mathematics Teacher, 61 (1968), 413.
- [88]
- Heath, Elements,
III, p. 269.
- [89]
- Heath, Elements,
III, p. 324.
- [90]
- Heath, Elements,
III, p. 364.
- [91]
- Heath, Elements,
III, p. 438-9.
- [92]
- Proclus,
p. 56 [68:20-22].
- [93]
- Heath, Elements,
III, p. 512-9.
- [94]
- Heath, Elements,
III, p. 519-20.
- Berggren, J. L.
- ``History of Greek Mathematics: A Survey of Recent Research.''
Historia Mathematica, 11 (1984), 394-410.
- Boyer, Carl B., and Uta C. Merzbach.
- A History of Mathematics.
2nd ed. New York: John Wiley & Sons, 1989.
- Bulmer-Thomas, Ivor.
- ``Euclid.''
DSB (1971).
- Dauben, Joseph W.
- The History of Mathematics from Antiquity to the Present /
A Selective Bibliography.
New York: Garland Publishing, Inc., 1985.
- Evans, George W.
- ``Postulates and Sequence in Euclid.''
The Mathematics Teacher, 20 (1927), 310-20.
- -----.
- ``Some of Euclid's Algebra.''
The Mathematics Teacher, 20 (1972), 121-41.
Rpt. The Mathematics Teacher, 61 (1968), 405-414.
- Gould, S. H.
- ``The Origins of Euclid's Axioms.''
The Mathematical Gazette, 46 (1962), 269-290.
- Heath, Sir Thomas L.
- A History of Greek Mathematics.
2 vols. 1921; rpt. New York: Dover Publications, Inc., 1981.
- -----.
- The Thirteen Books of Euclid's Elements.
2nd ed. 3 vols. 1926; rpt. New York: Dover Publications, Inc., 1956.
- Proclus.
- A Commentary on the First Book of Euclid's Elements.
Trans. Glenn R. Morrow. Princeton: PUP, 1970.
- Unguru, Sabetai.
- ``On the Need to Rewrite the History of Greek Mathematics.''
Archive for the History of Exact Sciences, 15 (1975), 67-114.
- Van der Waerden, B. L.
- Science Awakening I.
Trans. Arnold Dresden. Groningen, Holland: P. Noordhoff Ltd., [1975?].
jump to...
top of page
Outline of paper
text of paper
Suggestions for further study
Notes
Bibliography
Section:
Donald Lancon Jr /
Math & science
Next:
High school Euclid paper
Previous:
A little about myself
Donald Lancon Jr
[e-mail me]
Last modified:
Sat, Sep 15, 2001
![[figure from I.22]](IMAGES/euclid/eucli22.gif)
![[figure from I.47]](IMAGES/euclid/euclbrch.gif)
![[figure from II.5]](IMAGES/euclid/euclii5.gif)
![[figure from II.13]](IMAGES/euclid/euclii13.gif)
![[figure]](IMAGES/euclid/eucliii.gif)
![[figure from III.16]](IMAGES/euclid/eucliiix.gif)
![[figures from III.20, III.21, III.37]](IMAGES/euclid/eucliii3.gif)
![[figure from VI.29]](IMAGES/euclid/euclvi29.gif)
![[figure]](IMAGES/euclid/euclppps.gif)
![[figure]](IMAGES/euclid/eucl5rs.gif)