jump to
bottom of page
The
first part
of this page, ``A brief history of calculus'',
is a collection of notes I made as a prelude to
a History of Science paper that never happened.
(I did the
Euclid paper
instead.)
The
second part,
``Other interesting stuff'',
is just a collection of miscellaneous events in the history of math.
Citations appear in ``angle-brackets'' (e.g., <TT>).
The
list of sources
appears at the bottom of this page.
Ancient notions
- c.360 B.C.
-
Eudoxus of Cnidus
provides a
``method of exhaustion'',
close to the
limiting concept
of
calculus,
which is used by himself and
later Greeks
to find
areas
and
volumes
of
curvilinear
figures;
it was based on the
lemma
that
any
non-zero quantity
can be made as large as one wishes
by multiplying it by a large enough constant.
<HM>
Pre-calculus
- 1615
- Johannes Kepler
uses
infinitesimals
to calculate
volumes of revolution
in
Nova stereometria doliorum vinarorum
(``New Measurement of the
Volume
of Wine
Casks'').
<TT>
- 1635
- Bonaventura Cavalieri
calculates
volumes
using
infinitely small
sections.
<TT>
- 1655
- John Wallis
studies
infinite series
in
Arithmetica infinitorum
(``Arithmetic
of
Infinitesimals'')
<TT>
- 1658
- Blaise Pascal,
working on the
sine
function,
``almost'' discovers
calculus.
<TT>
Early calculus
- 1665
- Isaac Newton
retires to the country to escape the
Great Plague
in London;
there he invents the first form of
calculus.
<TT>
- 1668
- James Gregory
includes a geometrical version of
the
fundamental theorem of calculus
in
Geometriae pars universalis, inserviens quantitatum curvarum transmutationi & measurae
(``Geometrical Exercises and the Universal Part of
Geometry'').
<TT>
- 1669
- Newton
includes his method
for finding
areas under curves
in his
De analysi per equationes numero terminorum infinitas
(``On the Analysis of
Equations
Unlimited in the Number of Their Terms''),
circulated privately.
<TT>
- 1670
- Isaac Barrow
uses methods similar to
calculus
to draw
tangents
to curves,
find the
lengths of curves,
and the
areas bounded by curves.
<TT>
- 1675
- Gottfried Leibniz
introduces the
modern notation
![[elongated-S]](IMAGES/mathemat/integral.gif) for
integration
and the notation
dx/dy
for
differentiation;
he also determines the
product rule
for
differentiation.
<TT/MN>
for
integration
and the notation
dx/dy
for
differentiation;
he also determines the
product rule
for
differentiation.
<TT/MN>
- 1676
- Newton
writes two letters to
Leibniz,
hinting at his work with
infinite series
and
fluxions
(his form of
calculus);
also this year,
Leibniz
discovers how to
differentiate
any
fractional
power
of x.
<TT>
- 1677
- Leibniz
finds the
quotient rule
for
differentiation.
<TT>
Big-time calculus
- 1684
- Leibniz
publishes
``A new method for
maxima
and
minima
as well as
tangents,
which is impeded neither by
fractional
nor by
irrational
quantities,
and a remarkable type of
calculus
for this'';
although only six pages long, few can understand it.
<TT>
- 1686
- Leibniz
publishes his method of
integral calculus
in an issue of
Acta Eruditorum
(``Learned Works''?
-- my own translation, so might not be completely satisfactory).
<TT>
- 1691
- Michel Rolle
states without
proof
the
theorem
named after him.
<TT>
- 1693
- John Wallis
publishes
Newton's
method of
fluxions
in volume two of his
Opera Mathematica
(``Mathematical Works'').
<TT>
- 1694
- Jean Bernoulli
discovers the method known as
l'Hôpital's Rule
(a.k.a., l'Hospital's Rule);
it is known by that name because
Marquis Antoine de l'Hôpital
bought it from
Bernoulli
and introduced it in his influential 1696 textbook
Analyse des infiniment petits pour l'Intelligence des Lignes Courbes
(``Analysis of
Infinitesimals
for Understanding
Curved Lines''?? -- my own translation).
<TT>
- 1715
- Brook Taylor
introduces
his famous
series
in
Methodus incrementorum directa et inversa
(``Direct and Inverse Incremental Method''),
in which he develops the
calculus
of
finite differences.
<TT>
Later calculus
- 1797
- Joseph-Louis Lagrange introduces the notations
f'x and y'
for the derivatives of
f(x) and y,
respectively.
<MN/TT>
- 1800
- Louis F. A. Arbogast introduces the symbol D
for the operation of differentiation.
<MN/DC>
- 1841
- Carl Gustav Jacob Jacobi adopts the modern notation
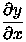 for partial differentiation;
Adrien-Marie Legendre originally introduced it in 1786,
but immediately abandoned it.
<MN/TT>
for partial differentiation;
Adrien-Marie Legendre originally introduced it in 1786,
but immediately abandoned it.
<MN/TT>
- 1854
- Bernhard Riemann defines the integral in a way
that does not require continuity.
<TT>
- 1872
- H. Eduard Heine, a student of Karl Weierstrass,
presents the modern ``epsilon-delta'' definition of a limit
in his Die Elemente der Functionenlehre
(``Elements of the Study of
Functions''??
-- my own translation).
<TT>
2000 B.C. to 200 B.C.
- c.1975 B.C.
- Mesopotamian mathematicians discover how to solve
quadratic equations.
<TT>
- c.1850 B.C.
- Mesopotamian mathematicians discover the so-called
Pythagorean theorem
approximately 12 centuries before the time of Pythagoras.
<TT>
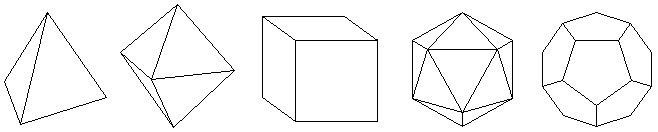
- c.465 B.C.
- The Pythagorean Hippasus of Metapontum discovers the dodecahedron,
a regular solid whose 12 faces are regular pentagons.
There are only 4 other regular solids:
the tetrahedron (4 equilateral triangles),
the cube (6 squares),
the octahedron (8 equilateral triangles),
and the icosahedron (20 equilateral triangles).
<TT/CR/HM>
- c.450 B.C.
- ``Achilles'' paradox of Zeno.
<HM>
- c.350 B.C.
- Menaechmus discovers the conic sections:
the parabola, ellipse, and hyperbola.
<HM>
- c.300 B.C.
- The thirteen books of Euclid's Elements
(the most widely read textbook ever written)
contains propositions on plane geometry,
the distributive, commutative, and associative laws of arithmetic,
quadratic equations,
prime numbers
(including the theorem that the set of primes is infinite),
perfect numbers, greatest common divisors, geometric series,
irrational numbers, and solid geometry,
including the five regular solids.
Unlike the modern treatment of these ideas,
the Greeks used an entirely geometrical approach in mathematics,
using line segments to represent all magnitudes (numbers).
Although the Elements compiles already-known
Greek mathematics,
some of the proofs are probably Euclid's own.
<HM>
See my
Euclid paper
for more information.
- c.250 B.C.
- Archimedes of Syracuse and the quadrature of the parabola.
<HM>
1500 A.D. to present
- 1575
- The first known proof by mathematical induction
is included in Francesco Maurolico's
Arithmeticorum Libri Duo;
he proves that the sum of the first n odd integers
is n^2.
<TT>
- 1635
- Rene Descartes discovers that any simple convex polyhedron
having V vertices, E edges, and F faces
obeys the rule V - E + F = 2;
since his discovery is not published until 1860,
the theorem is named after Leonhard Euler,
who rediscovered it in 1752.
<TT>
- 1679
- Gottfried Leibniz introduces binary arithmetic
in a letter written to Joachim Bouvet,
showing that any number may be expressed by 0's and 1's only.
<TT>
- 1781
- Joseph-Louis Lagrange expresses in a letter
to his mentor Jean le Rond d'Alembert
his fear that no further progress can be made in mathematics;
despite this dire prophesy,
many of his own contributions are still to come.
<TT>
- 1843
- While strolling along the Royal Canal,
Sir William Rowan Hamilton devises a mathematical system
which is not commutative;
he develops his idea into a system of ``quaternions'',
similar to that of three-dimensional vectors.
His ideas help to usher in modern abstract algebra.
<TT/HM>
- 1844
- Hermann Gunther-Grassman publishes
The Study of Extensions,
which deals with multidimensional vectors;
he almost single-handedly creates modern linear algebra.
<TT/HM>
- 1865
- August Ferdinand Mobius unveils his
single-sided, single-edged figure, the Mobius strip.
<TT>
- 1877
- Georg Cantor proves that the number of points on a line segment
is the same as the number of points in the interior of a square,
publication of the result is delayed for a year
because mathematicians refuse to believe it.
<TT>
- 1890
- Giuseppe Peano discovers a one-dimensional, continuous curve
that passes through all the points in the interior of a square.
<TT>
- 1902
- Bertrand Russell discovers his ``great paradox''.
<TT>
- 1908
- The final edition of Giuseppe Peano's
Mathematical Formulas contains about 4,200 theorems.
<TT>
- 1976
- Haken, Appel, and Koch prove with the use of a computer
that only four colors are required to color in any two-dimensional map
in such a way that no two adjacent regions share the same color;
this was conjectured in 1850 by Francis Guthrie.
<TT>
- <CR>
- CRC Standard Mathematical Tables, 26th edition
- William H. Beyer, ed. (CRC Press, 1981)
- <DC>
- The Historical Development of the Calculus
- C. H. Edwards, Jr. (Springer-Verlag, 1979)
- <MN>
- A History of Mathematical Notations/Volume II:
Notations Mainly in Higher Mathematics
- Florian Cajori (Open Court Publishing, 1952)
- <HM>
- A History of Mathematics, second edition
- Carl B. Boyer and Uta C. Merzbach (John Wiley & Sons, 1989)
- <HC>
- The History of the Calculus
and Its Conceptual Development
- Carl D. Boyer (Dover Publications, 1959)
- <TT>
- The Timetables of Science:
A Chronology of the Most Important People and Events
in the History of Science
- Alexander Hellemans and Bryan Bunch (Simon & Schuster, 1991)
jump to
top of page
Section:
Donald Lancon, Jr. /
Math & science
Next:
Some 20th-century scientists
Previous:
High school Euclid paper
Donald Lancon, Jr.
[e-mail me]
Last modified:
Thu, 26 Feb 2004
![[elongated-S]](IMAGES/mathemat/integral.gif) for
integration
and the notation
dx/dy
for
differentiation;
he also determines the
product rule
for
differentiation.
<TT/MN>
for
integration
and the notation
dx/dy
for
differentiation;
he also determines the
product rule
for
differentiation.
<TT/MN>
![[elongated-S]](IMAGES/mathemat/integral.gif) for
integration
and the notation
dx/dy
for
differentiation;
he also determines the
product rule
for
differentiation.
<TT/MN>
for
integration
and the notation
dx/dy
for
differentiation;
he also determines the
product rule
for
differentiation.
<TT/MN>
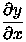 for partial differentiation;
Adrien-Marie Legendre originally introduced it in 1786,
but immediately abandoned it.
<MN/TT>
for partial differentiation;
Adrien-Marie Legendre originally introduced it in 1786,
but immediately abandoned it.
<MN/TT>
